Plot 95 Confidence Interval Python

Confidence Interval(CI) is essential in statistics and very important for data scientists. In this article, I will explain it thoroughly with necessary formulas and also demonstrate how to calculate it using python.

• Calculate Confidence Interval 95% Python
• Plot 95 Confidence Interval Pythonerval Python

Confidence Interval

Plot 95% confidence interval errorbar python pandas dataframes. June 17, 2017, at 9:31 PM. I want to show 95% confidence interval with Python pandas, matpolib. But I stucked, because for usual.std I would do smth like this. A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview.

As it sounds, the confidence interval is a range of values. In the ideal condition, it should contain the best estimate of a statistical parameter. It is expressed as a percentage. 95% confidence interval is the most common. You can use other values like 97%, 90%, 75%, or even 99% confidence interval if your research demands. Let’s understand it by an example:

Here is a statement:

“In a sample of 659 parents with toddlers, about 85%, stated they use a car seat for all travel with their toddler. From these results, a 95% confidence interval was provided, going from about 82.3% up to 87.7%.”

This statement means, we are 95% certain that the population proportion who use a car seat for all travel with their toddler will fall between 82.3% and 87.7%. If we take a different sample or a subsample of these 659 people, 95% of the time, the percentage of the population who use a car seat in all travel with their toddlers will be in between 82.3% and 87.7%.

Remember, 95% confidence interval does not mean 95% probability

The reason confidence interval is so popular and useful is, we cannot take data from all populations. Like the example above, we could not get the information from all the parents with toddlers. We had to calculate the result from 659 parents. From that result, we tried to get an estimate of the overall population. So, it is reasonable to consider a margin of error and take a range. That’s why we take a confidence interval which is a range.

We want a simple random sample and a normal distribution to construct a confidence interval. But if the sample size is large enough (30 or more) normal distribution is not necessary.

How to Calculate the Confidence Interval

The calculation of the confidence interval involves the best estimate which is obtained by the sample and a margin of error. So, we take the best estimate and add a margin of error to it. Here is the formula for the confidence interval and the margin of error:

Here, SE is the standard error.

Normally, CI is calculated for two statistical parameters: the proportion and the mean.

Combining these two formulas above, we can elaborate the formula for CI as follows:

Population proportion or the mean is calculated from the sample. In the example of “the parents with toddlers”, the best estimate or the population proportion of parents that uses car seats in all travel with their toddlers is 85%. So, the best estimate (population proportion) is 85. z-score is fixed for the confidence level (CL).

A z-score for a 95% confidence interval for a large enough sample size(30 or more) is 1.96.

Here are the z-scores for some commonly used confidence levels:

The method to calculate the standard error is different for population proportion and mean. The formula to calculate standard error of population proportion is:

The formula to calculate the standard error of the sample mean is:

As per the statement, the population proportion that uses a car seat for all travel with their toddlers is 85%. So, this is our best estimate. We need to add the margin of error to it. To calculate the margin of error we need the z-score and the standard error. I am going to calculate a 95% CI. The z-score should be 1.96 and I already mentioned the formula of standard error for the population proportion. Plugging in all the values:

The confidence interval is 82.3% and 87.7% as we saw in the statement before.

Confidence interval in Python

I am assuming that you are already a python user. But even if you are not a python user you should be able to get the concept of the calculation and use your own tools to calculate the same. The tools I used for this exercise are:

1. Jupyter Notebook environment.

If you install an anaconda package, you will get a Jupyter Notebook and the other tools as well. There are some good youtube videos to demonstrate how to install anaconda package if you do not have that already.

CI for the population Proportion in Python

I am going to use the Heart dataset from Kaggle. Please click on the link to download the dataset. First, I imported the packages and the dataset:

The last column of the data is ‘AHD’. It says if a person has heart disease or not. In the beginning, we have a ‘Sex’ column as well.

We are going to construct a CI for the female population proportion that has heart disease.

First, replace 1 and 0 with ‘Male’ and ‘Female’ in a new column ‘Sex1’.

We do not need all the columns in the dataset. We will only use the ‘AHD’ column as that contains if a person has heart disease or not and the Sex1 column we just created. Make a DataFrame with only these two columns and drop all the null values.

We need the number of females who have heart disease. The line of code below will give the number of males and females with heart disease and with no heart disease.

Here is the output table:

The number of females who have heart disease is 25. Calculate the female population proportion with heart disease.

The ‘p_fm’ is 0.26. The size of the female population:

The size of the female population is 97. Calculate the standard error

The standard error is 0.044.

Now construct the CI using the formulas above. The z-score is 1.96 for a 95% confidence interval.

The confidence interval is 0.17 and 0.344.

You can calculate it using the library ‘statsmodels’.

The confidence interval comes out to be the same as above.

CI for the Difference in Population Proportion

Is the population proportion of females with heart disease the same as the population proportion of males with heart disease? If they are the same, then the difference in both the population proportions will be zero.

We will calculate a confidence interval of the difference in the population proportion of females and males with heart disease.

Here is the step by step process:

Calculate the male population proportion with heart disease and standard error using the same procedure.

The male population proportion with heart disease is 0.55 and the male population size is 206. Calculate the standard error for the male population proportion.

The standard error for the male population is 0.034. Calculate the difference in standard error.

The difference in standard error is not just subtraction. Use proper formula.

Here is the formula to calculate the difference in two standard errors:

Let’s use this formula to calculate the difference in the standard error of male and female population with heart disease.

Use this standard error to calculate the difference in the population proportion of males and females with heart disease and construct the CI of the difference.

The CI is 0.18 and 0.4. This range does not have 0 in it. Both the numbers are above zero. So, We cannot make any conclusion that the population proportion of females with heart disease is the same as the population proportion of males with heart disease. If the CI would be -0.12 and 0.1, we could say that the male and female population proportion with heart disease is the same.

Calculation of CI of mean

We will use the same heart disease dataset. The dataset has a ‘chol’ column that contains the cholesterol level. For this demonstration,

we will calculate the confidence interval of the mean cholesterol level of the female population.

Let’s find the mean, standard deviation, and population size for the female population. I want to get the same parameters for the male population as well. Because it will be useful for our next exercise. Use pandas groupby and aggregate methods for this purpose. If you need a refresher on pandas groupby and aggregate method, please check out this article:

Here is the code to get the mean, standard deviation, and population size of the male and female population:

If we extract the necessary parameters for the female population only:

Here 1.96 is the z-score for a 95% confidence level.

Calculate the standard error using the formula for the standard error of the mean

Now we have everything to construct a CI for mean cholesterol in the female population.

Construct the CI

The CI came out to be 248.83 and 274.67.

That means the true mean of the cholesterol of the female population will fall between 248.83 and 274.67

Calculation of CI of The Difference in Mean

There are two approaches to calculate the CI for the difference in the mean of two populations.

Pooled approach and unpooled approach

As mentioned earlier, we need a simple random sample and a normal distribution. If the sample is large, a normal distribution is not necessary.

There is one more assumption for a pooled approach. That is, the variance of the two populations is the same or almost the same.

If the variance is not the same, the unpooled approach is more appropriate.

The formula of the standard error for the pooled approach is:

Here, s1 and s2 are the standard error for the population1 and population2. In the same way, n1 and n2 are the population size of population1 and population2.

The formula of the standard error for the unpooled approach is:

Here, we will construct the CI for the difference in mean of the cholesterol level of the male and female population.

We already derived all the necessary parameters from the dataset in the previous example. Here they are:

As we can see, the standard deviation of the two target populations is different. So. the variance must be different as well.

So, for this example, the unpooled approach will be more appropriate.

Calculate the standard error for male and female population using the formula we used in the previous example

The difference in mean of the two samples

The difference in mean ‘mean_d’ is 22.15.

Using the formula for the unpooled approach, calculate the difference in standard error:

Finally, construct the CI for the difference in mean

The lower and upper limit of the confidence interval came out to be 22.1494 and 22.15. They are almost the same. That means the mean cholesterol of the female population is not different than the mean cholesterol of the male population.

Conclusion

In this article, I tried to explain the confidence interval in detail with the calculation process in python. Python code I used here is simple enough for anyone to understand. Even if you are not a python user you should be able to understand the process and apply it in your way.

#statistcs #DataScience #DataAnalytics #ConfidenceInterval #Python

Autoregressive Integrated Moving Average (ARIMA) is a popular time series forecasting model. It is used in forecasting time series variable such as price, sales, production, demand etc.

1. Basics of ARIMA model

A) Autoregressive part

Autoregressive part refers to relationship between the variable (that we are trying to forecast) with its own lagged values. The order of AR term is denoted by p. If p=2, that means the variable depends upon past two lagged values. In case of seasonal ARIMA model, the seasonal AR part is denoted by the notation P.

• If P is let us say, 1, then that means the time series variable depends on the value for the same period during the last season. For example, if it is monthly data, then the value observed during March this year is dependent on value observed during last year March.
• While the non-seasonal AR order 2 indicates the value observed during March this year is dependent on value observed during February and January of this year.
• What will be the meaning of AR seasonal order P = 3 in case of monthly data? That means, if the present month is March, 2018 then time series value for this month is dependent on values during March 2017, March 2016 and March 2015.

The order of AR part can be inferred from the Partial Auto-Correlation Function (PACF) plot.

B) Integrated part

Integrated part refers to order of differencing. Non-seasonal differencing order is denoted by d and seasonal differencing order by D. Integrated part is essential when the series is non-stationary.

C) Moving Average part

In ARIMA model, Moving Average order indicates the dependence of present value of the time series variable on the lagged error terms. The non-seasonal MA order is denoted by q while the seasonal MA order is denoted by Q.
The order of MA part can be inferred from the Auto-Correlation Function (ACF) plot.
The following picture depicts a SARIMA model of the order (p,d,q)(P,D,Q)_m (Fore more on this).

SARIMA (p,d,q)(P,D,Q)m

where L is the backshift operator.

2. Example in Python

Using the famous Airline Passengers dataset, let us build the ARIMA model.

a) Auto-Correlation Function (ACF) plot

ACF plot with 99% Confidence Intervals

ACF plot with 95% Confidence Intervals

As you can see from these ACF plots, width of the confidence interval band decreases with increase in alpha value. These ACF plots and also the earlier line graph reveal that time series requires differencing (Further use ADF or KPSS tests)
If you want to get ACF values, then use the following code.

ACF values

b) Partial Auto-Correlation Function (PACF) plot

Now let us plot PACF.

c) Seasonal differencing

d) Fitting the model

i) ARIMA

ii) SARIMA

e) Diagnostic Plots

We want the residuals to be white noise process.

f) Forecasting

In case of ARIMA model, we can use the following code:
In case of SARIMA model, we need to use the following code:
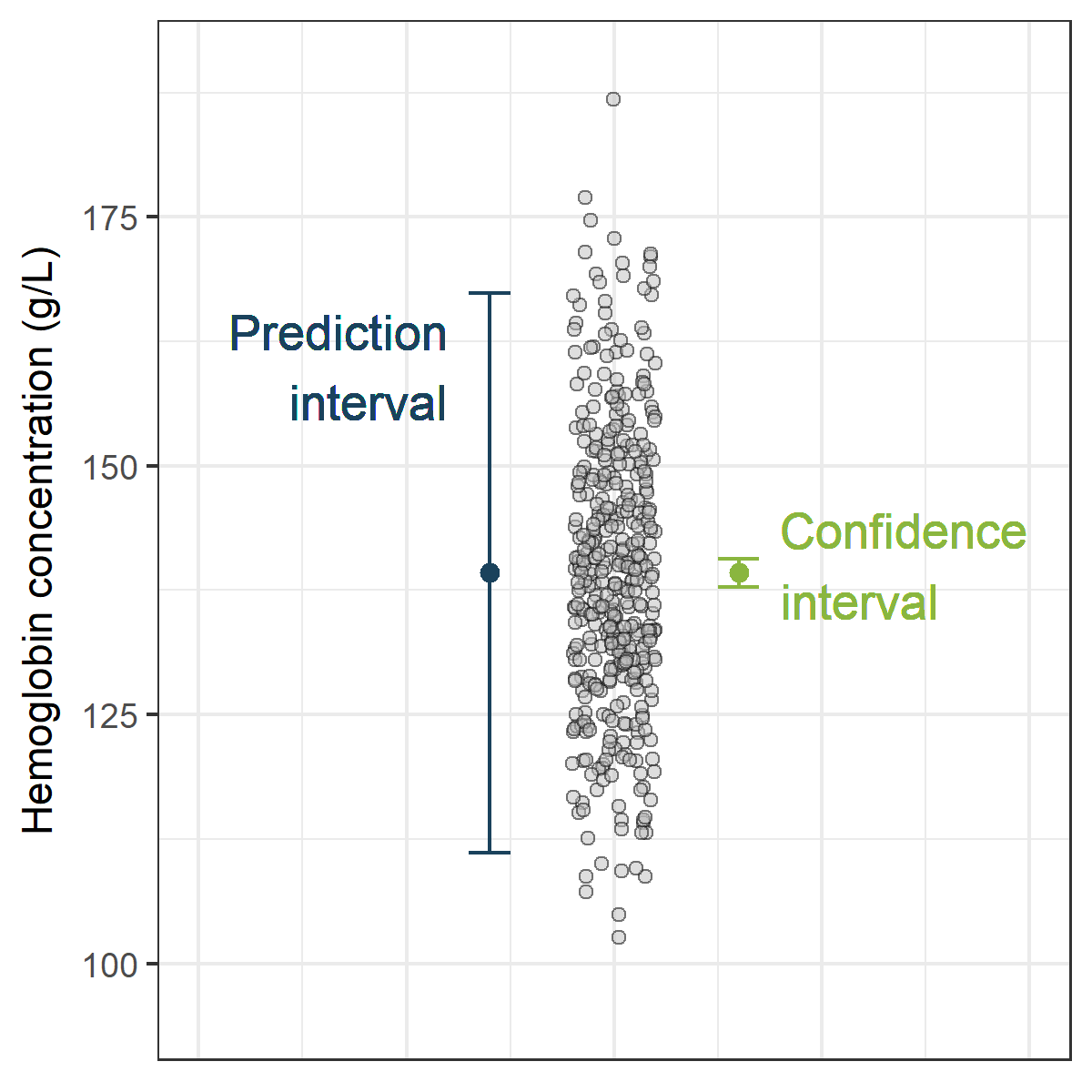
a) Forecast and confidence intervals

Or alternatively, we can get the prediction and confidence intervals for the predictions as shown below.

b) Plot the forecasted values and confidence intervals
For this, I have used the code from this blog-post, and modified it accordingly.

Further, we can use dynamic forecasting which uses the forecasted time series variable value instead of true time series value for prediction. But generally it does not perform as good as the normal static method.

Points to consider:

• Generally total order of differencing (d+D) should be not more than two.
• Even though we derive p and P values from PACF plots and q and Q values from ACF plots, we have to overfit, check residues, check performance. Model building is an art which requires us to consider various points before shortlisting the models.
• AIC should be used to compare the models with the same order of differencing (link).

Summary

Calculate Confidence Interval 95% Python

• the basics of ARIMA/SARIMA models and
• how to forecast using these models in Python

References

Plot 95 Confidence Interval Pythonerval Python